Parallel computing in Julia - M2PI edition
Friday, July 15
9:00am–12:00pm Mountain Time
Julia is a high-level programming language well suited for scientific computing and data science. Just-in-time compilation, among other things, makes Julia really fast yet interactive. For heavy computations, Julia supports multi-threaded and multi-process parallelism, both natively and via a number of external packages. It also supports memory arrays distributed across multiple processes either on the same or different nodes. In this hands-on workshop, we will start with a quick review of Julia’s multi-threading features but will focus primarily on Distributed standard library and its large array of tools. We will demo parallelization using two problems: a slowly converging series and a Julia set. We will run examples on a multi-core laptop and an HPC cluster.
Instructor: Alex Razoumov (SFU)
Software: All attendees will need a remote secure shell (SSH) client installed on their computer in order to
participate in the course exercises. On Windows we recommend
the free Home Edition of MobaXterm. On Mac and Linux computers SSH is
usually pre-installed (try typing ssh in a terminal to make sure it is there). No need to install Julia on your
computer.
Table of contents
Introduction to Julia language
- High-performance, dynamically typed programming language for scientific computing
- Uses just-in-time (JIT) compiler to compile all code, includes an interactive command line (REPL = read–eval–print loop, and can also be run in Jupyter), i.e. tries to combine the advantages of both compiled and interpreted languages
- Built-in package manager
- Lots of interesting design decisions, e.g. macros, support for Unicode, etc – covered in our introductory Julia course
- Support for parallel and distributed computing via its Standard Library and many 3rd party packages
- being added along the way, e.g. @threads were first introduced in v0.5
- currently under active development, both in features and performance
Running Julia locally
If you have Julia installed on your own computer, you can run it there: on a multi-core laptop/desktop you can launch multiple threads and processes and run them in parallel.
If you want to install Julia later on, you can find it here .
Using Julia on supercomputers
Julia on Compute Canada production clusters
Julia is among hundreds of software packages installed on the CC clusters. To use Julia on one of them, you would load the following module:
$ module load julia
Installing Julia packages on a production cluster
By default, all Julia packages you install from REPL will go into $HOME/.julia. If you want to put packages into
another location, you will need to (1) install inside your Julia session with (from within Julia):
empty!(DEPOT_PATH)
push!(DEPOT_PATH,"/scratch/path/to/julia/packages")
] add BenchmarkTools
and (2) before running Julia modify two variables (from the command line):
$ module load julia
$ export JULIA_DEPOT_PATH=/home/\$USER/.julia:/scratch/path/to/julia/packages
$ export JULIA_LOAD_PATH=@:@v#.#:@stdlib:/scratch/path/to/julia/packages
Don’t do this on the training cluster! We already have everything installed in a central location for all guest accounts.
Note: Some Julia packages rely on precompiled bits that developers think would work on all architectures,
but they don’t. For example, Plots package comes with several precompiled libraries, it installs without
problem on Compute Canada clusters, but then at runtime you will see an error about “GLIBC_2.18 not
found”. The proper solution would be to recompile the package on the cluster, but it is not done correctly
in Julia packaging, and the error persists even after “recompilation”. There is a solution for this, and you
can always contact us at support@tech.alliancecan.ca and ask for help. Another example if Julia’s NetCDF
package: it installs fine on Apple Silicon Macs, but it actually comes with a precompiled C package that was
compiled only for Intel Macs and does not work on M1.
Julia on the training cluster for this workshop
We have Julia on our training cluster kandinsky.c3.ca.
- one login node with 8 *"persistent"* cores and 30GB of memory,
- 60 compute nodes with 4 *"compute"* cores and 15GB of memory on each (240 cores in total)
In our introductory Julia course we use Julia inside a Jupyter notebook. Today we will be starting multiple threads and processes, with the eventual goal of running our workflows as batch jobs on an HPC cluster, so we’ll be using Julia from the command line.
Pause: We will now distribute accounts and passwords to connect to the cluster.
Normally, you would install Julia packages yourself. A typical package installation however takes several hundred MBs of RAM, a fairly long time, and creates many small files. Our training cluster runs on top of virtualized hardware with a shared filesystem. If several dozen workshop participants start installing packages at the same time, this will hammer the filesystem and will make it slow for all participants for quite a while.
Instead, for this workshop, you will run:
$ source /home/razoumov/shared/julia/config/loadJulia.sh
This script loads the Julia module and sets environment variables to point to a central environment in which we have pre-installed all the packages for this workshop.
Running Julia in the REPL
Where to run the REPL
You could now technically launch a Julia REPL (Read-Eval-Print-Loop). However, this would launch it on the login node and if everybody does this at the same time, we would probably stall our training cluster.
Instead, you will first launch an interactive job by running the Slurm command salloc:
$ salloc --mem-per-cpu=3600M --time=1:0:0
This puts you on a compute node for up to one hour.
Now you can launch the Julia REPL and try to run a couple of commands:
$ julia
_
_ _ _(_)_ | Documentation: https://docs.julialang.org
(_) | (_) (_) |
_ _ _| |_ __ _ | Type "?" for help, "]?" for Pkg help.
| | | | | | |/ _` | |
| | |_| | | | (_| | | Version 1.7.0 (2021-11-30)
_/ |\__'_|_|_|\__'_| |
|__/ |
julia> using BenchmarkTools
julia> @btime sqrt(2)
1.825 ns (0 allocations: 0 bytes)
1.4142135623730951
REPL modes
The Julia REPL has 4 modes:
julia> Julian mode to run code. Default mode. Go back to it from other modes with Backspace
help?> Help mode to access documentation. Enter it with ?
shell> Shell mode to run Bash commands. Enter it with ;
(env) pkg> Package manager mode to manage external packages. Enter it with ]
(env is the name of your current project environment.)
REPL keybindings
In the REPL, you can use standard command line (Emacs) keybindings:
C-c cancel
C-d quit
C-l clear console
C-u kill from the start of line
C-k kill until the end of line
C-a go to start of line
C-e go to end of line
C-f move forward one character
C-b move backward one character
M-f move forward one word
M-b move backward one word
C-d delete forward one character
C-h delete backward one character
M-d delete forward one word
M-Backspace delete backward one word
C-p previous command
C-n next command
C-r backward search
C-s forward search
REPL for parallel work
Remember our workflow to launch a Julia REPL:
# Step 0: start tmux (optional), gives you left-right panes, persistent terminal session
$ tmux
# Step 1: run the script to load our Julia environment with pre-installed packages
$ source /home/razoumov/shared/julia/config/loadJulia.sh
# Step 2: launch an interactive job on a compute node
$ salloc --mem-per-cpu=3600M --time=1:0:0
# Step 3: launch the Julia REPL
$ julia
This is great to run serial work.
When we will run parallel work however, we will want to use multiple CPUs per task in order to see a speedup.
So instead, you will run:
$ source /home/razoumov/shared/julia/config/loadJulia.sh
# Request 2 CPUs per task from Slurm
$ salloc --mem-per-cpu=3600M --cpus-per-task=2 --time=01:00:00
# Launch Julia on 2 threads
$ julia -t 2
Running scripts
Now, if we want to get an even bigger speedup, we could use even more CPUs per task. The problem is that our training cluster only has ~200 CPUs, so some of us would be left waiting for Slurm while the others can play with a bunch of CPUs for an hour. This is not an efficient approach. This is equally true on production clusters: if you want to run an interactive job using a lot of resources, you might have to wait for a long time.
A much better approach is to put our Julia code in a Julia script and run it through a batch job by using the
Slurm command sbatch.
Let’s save the following into a file job_script.sh:
#!/bin/bash
#SBATCH --ntasks=1
#SBATCH --cpus-per-task=4
#SBATCH --mem-per-cpu=3600M
#SBATCH --time=00:10:00
julia -t 4 julia_script.jl
Then we submit our job script:
$ sbatch job_script.sh
Serial Julia features worth noting in 10 mins
JIT compilation
Programming languages are either interpreted or compiled.
Interpreted languages use interpreters: programs that execute your code directly (Python, for instance, uses the interpreter CPython, written in C). Interpreted languages are very convenient since you can run sections of your code as soon as you write them. However, they are slow.
Compiled languages use compilers: programs that translate your code into machine code. Machine code is extremely efficient, but of course, having to compile your code before being able to run it makes for less convenient workflows when it comes to writing or debugging code.
Julia uses just-in-time compilation or JIT based on LLVM : the source code is compiled at run time. This combines the flexibility of interpretation with the speed of compilation, bringing speed to an interactive language. It also allows for dynamic recompilation, continuous weighing of gains and costs of the compilation of parts of the code, and other on the fly optimizations.
Here is a great blog post covering this topic if you want to dive deeper into the functioning of JIT compilers.
Macros
In the tradition of Lisp, Julia has strong metaprogramming capabilities , in particular in the form of macros.
Macros are parsed and evaluated first, then their output gets evaluated like a classic expression. This allows the language to modify itself in a reflective manner.
Macros have a @ prefix and are defined with a syntax similar to that of functions.
@time for instance is a macro that executes an expression and prints the execution time and other information.
Fun fact
Julia supports unicode
. In a Julia REPL,
type  , followed by the TAB key, and you get 🐌.
, followed by the TAB key, and you get 🐌.
While assigning values to a “snail variable” might not be all that useful, a wide access to—for instance—Greek letters, makes Julia’s code look nicely similar to the equations it represents. For instance, if you type TAB after each variable name, the following:
\pgamma = ((\alpha \pi + \beta) / \delta) + \upepsilon
looks like:
ɣ = ((α π + β) / δ) + ε
In Julia you can omit the multiplication sign in some cases, e.g.
julia> 2π
6.283185307179586
Intro to parallelism
Threads vs. processes
In Unix a process is the smallest independent unit of processing, with its own memory space – think of an instance of a running application. The operating system tries its best to isolate processes so that a problem with one process doesn’t corrupt or cause havoc with another process. Context switching between processes is relatively expensive.
A process can contain multiple threads, each running on its own CPU core (parallel execution), or sharing CPU cores if there are too few CPU cores relative to the number of threads (parallel + concurrent execution). All threads in a Unix process share the virtual memory address space of that process, e.g. several threads can update the same variable, whether it is safe to do so or not (we’ll talk about thread-safe programming in this course). Context switching between threads of the same process is less expensive.
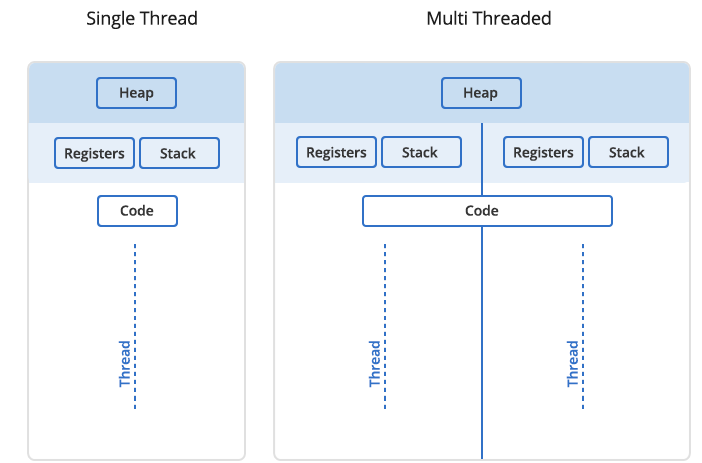
- Threads within a process communicate via shared memory, so multi-threading is always limited to shared memory within one node.
- Processes communicate via messages (over the cluster interconnect or via shared memory). Multi-processing can be in shared memory (one node, multiple CPU cores) or distributed memory (multiple cluster nodes). With multi-processing there is no scaling limitation, but traditionally it has been more difficult to write code for distributed-memory systems. Julia tries to simplify it with high-level abstractions.
In Julia you can parallelize your code with multiple threads, or with multiple processes, or both (hybrid parallelization).
Discussion
What are the benefits of each: threads vs. processes? Consider (1) context switching, e.g. starting and terminating or concurrent execution, (2) communication, (3) scaling up.
Parallelism in Julia
The main goal of this course is to teach you the basic tools for parallel programming in Julia, targeting both multi-core PCs and distributed-memory clusters. We will cover the following topics:
- multi-threading with Base.Threads
- multi-processing with Distributed.jl
- DistributedArrays.jl—distributing large arrays across multiple processes
We will not be covering the following topics today:
- SharedArrays.jl—shared-memory access to large arrays from multiple processes
- ThreadsX.jl
- ClusterManagers.jl
- Concurrent function calls (“lightweight threads” for suspending/resuming computations)
- MPI.jl—a port of the standard MPI library to Julia
- MPIArrays.jl
- LoopVectorization.jl
- FLoops.jl
- Transducers.jl
- Dagger.jl—a task graph scheduler heavily inspired by Python’s Dask
- DistributedData.jl
- GPU-related packages
Multi-threading with Base.Threads (slow series)
Important: Today we are working on a compute node inside an interactive job scheduled with salloc. Do not run
Julia on the login node!
Let’s start Julia by typing julia in bash:
using Base.Threads # otherwise would have to preface all functions/macros with 'Threads.'
nthreads() # by default, Julia starts with a single thread of execution
If instead we start with julia -t 4 (or prior to v1.5 with JULIA_NUM_THREADS=4 julia):
using Base.Threads
nthreads() # now we have access to 4 threads
When launched from this interface, these four threads will run on several CPU cores on a compute node – likely a
combination of concurrent and parallel execution, especially considering the restrictions from your salloc job.
Let’s run our first multi-threaded code:
@threads for i=1:10 # parallel for loop using all threads
println("iteration $i on thread $(threadid())") # notice bash-like syntax
end
This would split the loop between 4 threads running on two CPU cores: each core would be taking turns running two of your threads (and maybe threads from other users).
Let’s now fill an array with values in parallel:
a = zeros(Int32, 10) # 32-bit integer array
@threads for i=1:10
a[i] = threadid() # should be no collision: each thread writes to its own part
end
a
Here we are filling this array in parallel, and no thread will overwrite another thread’s result. In other words, this code is thread-safe.
Note: @threads macro is well-suited for shared-memory data parallelism without any reduction. Curiously, @threads does not have any data reduction built-in, which is a serious omission that will likely be addressed in future versions.
Let’s initialize a large floating array:
nthreads() # still running 4 threads
n = Int64(1e8) # integer number
a = zeros(n);
typeof(a) # how much memory does this array take?
and then fill it with values using a single thread, and time this operation:
@time for i in 1:n
a[i] = log10(i)
end
On the training cluster I get 14.38s, 14.18s, 14.98s with one thread.
Note: There is also
@btimefrom BenchmarkTools package that has several advantages over@time. We will switch to it soon.
Let’s now time parallel execution with 4 threads on 2 CPU cores:
using Base.Threads
@time @threads for i in 1:n
a[i] = log10(i)
end
On the training cluster I get 6.57s, 6.19s, 6.10s – this is ~2X speedup, as expected.
Let’s add reduction
We will compute the sum with multiple threads. Consider this code:
total = 0
@threads for i = 1:Int(1e6)
global total += i # use `total` from global scope
end
println("total = ", total)
This code is not thread-safe:
- race condition: multiple threads updating the same variable at the same time
- a new result every time
- unfortunately,
@threadsdoes not have built-in reduction support
Let’s make it thread-safe (one of many possible solutions) using an atomic variable total. Only one
thread can update an atomic variable at a time; all other threads have to wait for this variable to be
released before they can write into it.
total = Atomic{Int64}(0)
@threads for i in 1:Int(1e6)
atomic_add!(total, i)
end
println("total = ", total[]) # need to use [] to access atomic variable's value
Now every time we get the same result. This code is supposed to be much slower: threads are waiting for others to finish updating the variable, so with 4 threads and one variable there should be a lot of waiting … Atomic variables were not really designed for this type of usage … Let’s do some benchmarking!
Benchmarking in Julia
We already know that we can use @time macro for timing our code. Let’s do summation of integers from 1 to Int64(1e8)
using a serial code:
n = Int64(1e8)
total = Int128(0) # 128-bit for the result!
@time for i in 1:n
global total += i
end
println("total = ", total)
On the training cluster I get 10.87s, 10.36s, 11.07s. Here @time also includes JIT compilation time
(marginal here). Let’s switch to @btime from BenchmarkTools: it runs the code several times, reports the
shortest time, and prints the result only once. Therefore, with @btime you don’t need to precompile the
code.
using BenchmarkTools
n = Int64(1e8)
total = Int128(0) # 128-bit for the result!
@btime for i in 1:n
global total += i
end
println("total = ", total)
10.865 s
Next we’ll package this code into a function:
function quick(n)
total = Int128(0) # 128-bit for the result!
for i in 1:n
total += i
end
return(total)
end
@btime quick(Int64(1e8)) # correct result, 1.826 ns runtime
@btime quick(Int64(1e9)) # correct result, 1.825 ns runtime
@btime quick(Int64(1e15)) # correct result, 1.827 ns runtime
In all these cases we see ~2 ns running time – this can’t be correct! What is going on here? It turns out that Julia is replacing the summation with the exact formula !
We want to:
- force computation we’ll compute something more complex than simple integer summation, so that it cannot be replaced with a formula
- exclude compilation time we’ll package the code into a function + precompile it
- make use of optimizations for type stability package into a function + precompile it
- time only the CPU-intensive loops
Slow series
We could replace integer summation with the harmonic series, however, the traditional harmonic series diverges. It turns out that if we omit the terms whose denominators in decimal notation contain any digit or string of digits, it converges, albeit very slowly (Schmelzer & Baillie 2008), e.g.

But this slow convergence is actually good for us: our answer will be bounded by the exact result (22.9206766192…) on the upper side. We will sum all the terms whose denominators do not contain the digit “9”.
We will have to check if “9” appears in each term’s index i. One way to do this would be checking for a substring in a
string:
if !occursin("9", string(i))
<add the term>
end
It turns out that integer exclusion is ∼4X faster (thanks to Paul Schrimpf from the Vancouver School of Economics @UBC for this code!):
function digitsin(digits::Int, num) # decimal representation of `digits` has N digits
base = 10
while (digits ÷ base > 0) # `digits ÷ base` is same as `floor(Int, digits/base)`
base *= 10
end
# `base` is now the first Int power of 10 above `digits`, used to pick last N digits from `num`
while num > 0
if (num % base) == digits # last N digits in `num` == digits
return true
end
num ÷= 10 # remove the last digit from `num`
end
return false
end
if !digitsin(9, i)
<add the term>
end
Let’s now do the timing of our serial summation code with 1e8 terms:
function slow(n::Int64, digits::Int)
total = Float64(0) # this time 64-bit is sufficient!
for i in 1:n
if !digitsin(digits, i)
total += 1.0 / i
end
end
return total
end
@btime slow(Int64(1e8), 9) # total = 13.277605949858103, runtime 2.986 s
1st multi-threaded version: using an atomic variable
Recall that with an atomic variable only one thread can write to this variable at a time: other threads have to wait before this variable is released, before they can write. With several threads running in parallel, there will be a lot of waiting involved, and the code should be relatively slow.
using Base.Threads
using BenchmarkTools
function slow(n::Int64, digits::Int)
total = Atomic{Float64}(0)
@threads for i in 1:n
if !digitsin(digits, i)
atomic_add!(total, 1.0 / i)
end
end
return total[]
end
@btime slow(Int64(1e8), 9)
Exercise “Threads.1”
Put this version of
slow()along withdigitsin()into the fileatomicThreads.jland run it from the bash terminal (or from from REPL). First, time this code with 1e8 terms using one thread (serial runjulia atomicThreads.jl). Next, time it with 2 or 4 threads (parallel runjulia -t 2 atomicThreads.jl). Did you get any speedup? Make sure you obtain the correct numerical result.
With one thread I measured 2.838 s. The runtime stayed essentially the same (now we are using atomic_add()) which
makes sense: with one thread there is no waiting for the variable to be released.
With four threads, I measured 5.261 s – let’s discuss! Is this what we expected?
Exercise “Threads.2”
Let’s run the previous exercise as a batch job with
sbatch. Hint: you will need to go to the login node and submit a multi-core job withsbatch shared.sh. When finished, do not forget to go back to (or restart) your interactive job.
2nd version: alternative thread-safe implementation
In this version each thread is updating its own sum, so there is no waiting for the atomic variable to be released? Is this code faster?
using Base.Threads
using BenchmarkTools
function slow(n::Int64, digits::Int)
total = zeros(Float64, nthreads())
@threads for i in 1:n
if !digitsin(digits, i)
total[threadid()] += 1.0 / i
end
end
return sum(total)
end
@btime slow(Int64(1e8), 9)
Update: Pierre Fortin brought to our attention the
false sharing effect. It arises when several threads are
writing into variables placed close enough to each other to end up in the same cache line. Cache lines
(typically ~32-128 bytes in size) are chunks of memory handled by the cache. If any two threads are updating
variables (such as two neighbouring elements in our total array here) that end up in the same cache line,
the cache line will have to migrate between the two threads’ caches, reducing the performance.
In general, you want to align shared global data (thread partitions in the array total in our case) to
cache line boundaries, or avoid storing thread-specific data in an array indexed by the thread id or
rank. Pierre suggested a solution using the function space() which introduces some spacing between array
elements so that data from different threads do not end up in the same cache line:
using Base.Threads
using BenchmarkTools
function digitsin(digits::Int, num) # decimal representation of `digits` has N digits
base = 10
while (digits ÷ base > 0) # `digits ÷ base` is same as `floor(Int, digits/base)`
base *= 10
end
# `base` is now the first Int power of 10 above `digits`, used to pick last N digits from `num`
while num > 0
if (num % base) == digits # last N digits in `num` == digits
return true
end
num ÷= 10 # remove the last digit from `num`
end
return false
end
# Our initial function:
function slow(n::Int64, digits::Int)
total = zeros(Float64, nthreads())
@threads for i in 1:n
if !digitsin(digits, i)
total[threadid()] += 1.0 / i
end
end
return sum(total)
end
# Function optimized to prevent false sharing:
function space(n::Int64, digits::Int)
space = 8 # assume a 64-byte cache line, hence 8 Float64 elements per cache line
total = zeros(Float64, nthreads()*space)
@threads for i in 1:n
if !digitsin(digits, i)
total[threadid()*space] += 1.0 / i
end
end
return sum(total)
end
@btime slow(Int64(1e8), 9)
@btime space(Int64(1e8), 9)
Here are the timings from two successive calls to slow() and space() on the the training cluster:
[~/tmp]$ julia separateSums.jl
2.836 s (7 allocations: 656 bytes)
2.882 s (7 allocations: 704 bytes)
[~/tmp]$ julia -t 4 separateSums.jl
935.609 ms (23 allocations: 2.02 KiB)
687.972 ms (23 allocations: 2.23 KiB)
[~/tmp]$ julia -t 10 separateSums.jl
608.226 ms (53 allocations: 4.73 KiB)
275.662 ms (54 allocations: 5.33 KiB)
The speedup is substantial!
We see similar speedup with space = 4, but not quite with space = 2, suggesting that we are dealing with
32-byte cache lines on our system.
3rd multi-threaded version: using heavy loops
This version is classical task parallelism: we divide the sum into pieces, each to be processed by an
individual thread. For each thread we explicitly compute the start and finish indices it processes.
using Base.Threads
using BenchmarkTools
function slow(n::Int64, digits::Int)
numthreads = nthreads()
threadSize = floor(Int64, n/numthreads) # number of terms per thread (except last thread)
total = zeros(Float64, numthreads);
@threads for threadid in 1:numthreads
local start = (threadid-1)*threadSize + 1
local finish = threadid < numthreads ? (threadid-1)*threadSize+threadSize : n
println("thread $threadid: from $start to $finish");
for i in start:finish
if !digitsin(digits, i)
total[threadid] += 1.0 / i
end
end
end
return sum(total)
end
@btime slow(Int64(1e8), 9)
Let’s time this version together with heavyThreads.jl: 984.076 ms – is this the fastest version?
Exercise “Threads.3”
Would the runtime be different if we use 2 threads instead of 4?
Finally, below are the timings on Cedar with heavyThreads.jl. Note that the times reported here were
measured with 1.6.2. Going from 1.5 to 1.6, Julia saw quite a big improvement (~30%) in performance, plus a
CPU on Cedar is different from a vCPU on the training cluster, so treat these numbers only as relative to each
other.
#!/bin/bash
#SBATCH --ntasks=1
#SBATCH --cpus-per-task=...
#SBATCH --mem-per-cpu=3600M
#SBATCH --time=00:10:00
#SBATCH --account=def-someuser
module load julia
julia -t $SLURM_CPUS_PER_TASK heavyThreads.jl
| Code | serial | 2 cores | 4 cores | 8 cores | 16 cores |
| Time | 7.910 s | 4.269 s | 2.443 s | 1.845 s | 1.097 s |
Task parallelism with Base.Threads: building a dynamic scheduler
In addition to @threads (automatically parallelize a loop with multiple threads), Base.Threads includes
Threads.@spawn that runs a task (an expression / function) on any available thread and then immediately
returns to the main thread.
Consider this:
using Base.Threads
import Base.Threads: @spawn # has to be explicitly imported to avoid potential conflict with Distributed.@spawn
nthreads() # make sure you have access to multiple threads
threadid() # always shows 1 = local thread
fetch(@spawn threadid()) # run this function on another available thread and get the result
Every time you run this, you will get a semi-random reponse, e.g.
for i in 1:30
print(fetch(@spawn threadid()), " ")
end
You can think of @spawn as a tool to dynamically offload part of your computation to another thread – this is
classical task parallelism, unlike @threads which is data parallelism.
With @spawn it is up to you to write an algorithm to subdivide your computation into multiple threads. With
a large loop, one possibility is to divide the loop into two pieces, offload the first piece to another thread
and run the other one locally, and then recursively subdivide these pieces into smaller chunks. With N
subdivisions you will have 2^N tasks running on a fixed number of threads, and only one of these tasks will
not be scheduled with @spawn.
using Base.Threads
import Base.Threads: @spawn
using BenchmarkTools
function digitsin(digits::Int, num)
base = 10
while (digits ÷ base > 0)
base *= 10
end
while num > 0
if (num % base) == digits
return true
end
num ÷= 10
end
return false
end
@doc """
a, b are the left and right edges of the current interval;
numsubs is the number of subintervals, each will be assigned to a thread;
numsubs will be rounded up to the next power of 2,
i.e. setting numsubs=5 will effectively use numsubs=8
""" ->
function slow(n::Int64, digits::Int, a::Int64, b::Int64, numsubs=16)
if b-a > n/numsubs
mid = (a+b)>>>1 # shift by 1 bit to the right
finish = @spawn slow(n, digits, a, mid, numsubs)
t2 = slow(n, digits, mid+1, b, numsubs)
return fetch(finish) + t2
end
t = Float64(0)
println("computing on thread ", threadid())
for i in a:b
if !digitsin(digits, i)
t += 1.0 / i
end
end
return t
end
n = Int64(1e8)
@btime slow(n, 9, 1, n, 1) # run the code in serial (one interval, use one thread)
@btime slow(n, 9, 1, n, 4) # 4 intervals, each scheduled to run on 1 of the threads
@btime slow(n, 9, 1, n, 16) # 16 intervals, each scheduled to run on 1 of the threads
With four threads and numsubs=4, in one of my tests the runtime went down from 2.986 s (serial) to 726.044
ms. However, depending on the number of subintervals, Julia might decide not to use all four threads!
Consider this:
julia> nthreads()
4
julia> n = Int64(1e9)
1000000000
julia> @btime slow(n, 9, 1, n, 1) # serial run (one interval, use one thread)
computing on thread 1
computing on thread 1
computing on thread 1
computing on thread 1
29.096 s (12 allocations: 320 bytes)
14.2419130103833
julia> @btime slow(n, 9, 1, n, 4) # 4 intervals
computing on thread 1 - this line was printed 4 times
computing on thread 2 - this line was printed 5 times
computing on thread 3 - this line was printed 6 times
computing on thread 4 - this line was printed once
14.582 s (77 allocations: 3.00 KiB)
14.2419130103818
julia> @btime slow(n, 9, 1, n, 128) # 128 intervals
computing on thread 1 - this line was printed 132 times
computing on thread 2 - this line was printed 130 times
computing on thread 3 - this line was printed 131 times
computing on thread 4 - this line was printed 119 times
11.260 s (2514 allocations: 111.03 KiB)
14.24191301038047
Parallelizing the Julia set with Base.Threads
The project is the mathematical problem to compute a Julia set – no relation to Julia language! A Julia set is defined as a set of points on the complex plane that remain bound under infinite recursive transformation . We will use the traditional form , where is a complex constant. Here is our algorithm:
- pick a point
- compute iterations until (arbitrary fixed radius; here is a complex constant)
- store the iteration number at which reaches the circle
- limit max iterations at 255
4.1 if , then is a stable point
4.2 the quicker a point diverges, the lower its is - plot for all in a rectangular region ,
We should get something conceptually similar to this figure (here ; we’ll get drastically different fractals for different values of ):

Note: you might want to try these values too:
- original textbook example
- and 1.5X zoom-out denser spirals
- and 1.8X zoom-out beans
- and 1.2X zoom-out connected spiral boots
Below is the serial code juliaSetSerial.jl. If you are running Julia on your own computer, make sure you
have the required packages:
] add BenchmarkTools
] add Plots
Let’s study the code:
using BenchmarkTools
function pixel(z)
c = 0.355 + 0.355im
z *= 1.2 # zoom out
for i = 1:255
z = z^2 + c
if abs(z) >= 4
return i
end
end
return 255
end
const height, width = repeat([2_000],2) # 2000^2 image
println("Computing Julia set ...")
const stability = zeros(Int32, height, width);
@btime for i in 1:height, j in 1:width
point = (2*(j-0.5)/width-1) + (2*(i-0.5)/height-1)im # rescale to -1:1 in the complex plane
stability[i,j] = pixel(point)
end
println("Plotting to PNG ...")
using Plots
gr() # initialize the gr backend
ENV["GKSwstype"] = "100" # operate in headless mode
fname = "$(height)x$(width)"
png(heatmap(stability, size=(width,height), color=:gist_ncar), fname)
Let’s run this code with julia juliaSetSerial.jl. On my laptop it reports 931.024 ms.
function juliaSet(height, width)
stability = zeros(Int32, height, width);
for i in 1:height, j in 1:width
point = (2*(j-0.5)/width-1) + (2*(i-0.5)/height-1)im # rescale to -1:1 in the complex plane
stability[i,j] = pixel(point)
end
end
println("Computing Julia set ...")
@btime juliaSet(2000, 2000)
println("Writing NetCDF ...")
using NetCDF
filename = "test.nc"
isfile(filename) && rm(filename)
nccreate(filename, "stability", "x", collect(1:height), "y", collect(1:width), t=NC_INT, mode=NC_NETCDF4, compress=9);
ncwrite(stability, filename, "stability");
This code will produce the file test.nc that you can download to your computer and render with ParaView or
other visualization tool.
Exercise “Fractal.1”
Try one of these:
- With NetCDF output, compare the expected and actual file sizes.
- Try other values of the parameter (see above).
- Increase the problem size from the default . Will you have enough physical memory for ? How does this affect the runtime?
If computing takes forever, recall that
@btimeruns the code multiple times, while@timedoes it only once. Also, you might like a progress bar inside the terminal:using ProgressMeter @showprogress <for loop>
Parallelizing
- Load Base.Threads.
- Add
@threadsbefore the outer loop, and time this parallel loop.
On my laptop with 8 threads the timing is 193.942 ms (4.8X speedup) which is good but not great – certainly worse than linear speedup … The speedup on the training cluster is not great either. There could be several potential problems:
- False sharing effect (cache issues with multiple threads writing into adjacent array elements).
- Less than perfect load balancing between different threads.
- Row-major vs. column-major loop order for filling in the
stabilityarray. - Some CPU cores are lower efficiency, and they are slowing down the whole calculation.
Take-home exercise “Fractal.2”
How would you fix this issue? If you manage to get a speedup closer to 8X with Base.Threads on 8 cores, we would love to hear your solution! Please only check the solution once you work on the problem yourself.
Take-home exercise “Fractal.3”
Build a 3D cube based on the Julia set where the 3rd axis would be a slowly varying
cconstant. For example, try to interpolate linearly between and , or between any other two complex values. Send us an animation traversing your volume once you are done. What cube resolution did you achieve?
Distributed.jl: basics
Parallelizing with multiple Unix processes (MPI tasks)
Julia’s Distributed package provides multiprocessing environment to allow programs to run on multiple processors in shared or distributed memory. On each CPU core you start a separate Unix / MPI process, and these processes communicate via messages. Unlike in MPI, Julia’s implementation of message passing is one-sided, typically with higher-level operations like calls to user functions on a remote process.
- a remote call is a request by one processor to call a function on another processor; returns a remote/future reference
- the processor that made the call proceeds to its next operation while the remote call is computing, i.e. the call is non-blocking
- you can obtain the remote result with
fetch()or make the calling processor block withwait()
In this workflow you have a single control process + multiple worker processes. Processes pass information via messages underneath, not via variables in shared memory.
Launching worker processes
There are three different ways you can launch worker processes:
- with a flag from bash:
julia -p 8 # open REPL, start Julia control process + 8 worker processes
julia -p 8 code.jl # run the code with Julia control process + 8 worker processes
- from a job submission script:
#!/bin/bash
#SBATCH --ntasks=8
#SBATCH --cpus-per-task=1
#SBATCH --mem-per-cpu=3600M
#SBATCH --time=00:10:00
#SBATCH --account=def-someuser
srun hostname -s > hostfile # parallel I/O
sleep 5
module load julia/1.7.0
julia --machine-file ./hostfile ./code.jl
- from the control process, after starting Julia as usual with
julia:
using Distributed
addprocs(8)
Note: All three methods launch workers, so combining them will result in 16 (or 24!) workers (probably not the best idea). Select one method and use it.
With Slurm, methods (1) and (3) work very well, so—when working on a CC cluster—usually there is no need to construct a machine file.
Process control
Let’s start an interactive MPI job:
source /home/razoumov/shared/julia/config/loadJulia.sh
salloc --mem-per-cpu=3600M --time=01:00:00 --ntasks=4
Inside this job, start Julia with julia (single control process).
using Distributed
addprocs(4) # add 4 worker processes; this might take a while on the training cluster
println("number of cores = ", nprocs()) # 5 cores
println("number of workers = ", nworkers()) # 4 workers
workers() # list worker IDs
You can easily remove selected workers from the pool:
rmprocs(2, 3, waitfor=0) # remove processes 2 and 3 immediately
workers()
or you can remove all of them:
for i in workers() # cycle through all workers
t = rmprocs(i, waitfor=0)
wait(t) # wait for this operation to finish
end
workers()
interrupt() # will do the same (remove all workers)
addprocs(4) # add 4 new worker processes (notice the new IDs!)
workers()
Discussion
If from the control process we start workers, where will these processes run? Consider the following cases:
- a laptop with 2 CPU cores,
- a cluster login node with 16 CPU cores,
- a cluster Slurm job with 4 CPU cores.
Remote calls
Let’s restart Julia with julia (single control process).
using Distributed
addprocs(4) # add 4 worker processes
Let’s define a function on the control process and all workers and run it:
@everywhere function showid() # define the function everywhere
println("my id = ", myid())
end
showid() # run the function on the control process
@everywhere showid() # run the function on the control process + all workers
@everywhere does not capture any local variables (unlike @spawnat that we’ll study below), so on workers we don’t
see any variables from the control process:
x = 5 # local (control process only)
@everywhere println(x) # get errors: x is not defined elsewhere
However, you can still obtain the value of x from the control process by using this syntax:
@everywhere println($x) # use the value of `x` from the control process
The macro that we’ll use a lot today is @spawnat. If we type:
a = 12
@spawnat 2 println(a) # will print 12 from worker 2
it will do the following:
- pass the namespace of local variables to worker 2
- spawn function execution on worker 2
- return a Future handle (referencing this running instance) to the control process
- return the REPL to the control process (while the function is running on worker 2), so we can continue running commands
Now let’s modify our code slightly:
a = 12
@spawnat 2 a+10 # Future returned but no visible calculation
There is no visible calculation happening; we need to fetch the result from the remote function before we can print it:
r = @spawnat 2 a+10
typeof(r)
fetch(r) # get the result from the remote function; this will pause
# the control process until the result is returned
You can combine both @spawnat and fetch() in one line:
fetch(@spawnat 2 a+10) # combine both in one line; the control process will pause
@fetchfrom 2 a+10 # shorter notation; exactly the same as the previous command
Exercise “Distributed.1”
Try to define and run a function on one of the workers, e.g.
function cube(x) return x*x*x endHint: Use
@everywhereto define the function on all workers. Julia may not have a high-level mechanism to define a function on a specific worker, short of loading that function as a module from a file. Something like this@fetchfrom 2 function cube(x) return x*x*x enddoes not seem to have any effect.
Exercise “Distributed.2”
Now run the same function on all workers, but not on the control process. Hint: use
workers()to cycle through all worker processes andprintln()to print from each worker.
You can also spawn computation on any available worker:
r = @spawnat :any log10(a) # start running on one of the workers
fetch(r)
Back to the slow series: serial code
Let’s restart Julia with julia -p 2 (control process + 2 workers). We’ll start with our serial code (below), save it as serialDistributed.jl, and run it.
using Distributed
using BenchmarkTools
@everywhere function digitsin(digits::Int, num)
base = 10
while (digits ÷ base > 0)
base *= 10
end
while num > 0
if (num % base) == digits
return true
end
num ÷= 10
end
return false
end
@everywhere function slow(n::Int64, digits::Int)
total = Int64(0)
for i in 1:n
if !digitsin(digits, i)
total += 1.0 / i
end
end
return total
end
@btime slow(Int64(1e8), 9) # serial run: total = 13.277605949858103
For me this serial run takes 3.192 s on the training cluster. Next, let’s run it on 3 (control + 2 workers) cores simultaneously:
@everywhere using BenchmarkTools
@everywhere @btime slow(Int64(1e8), 9) # runs on 3 (control + 2 workers) cores simultaneously
Here we are being silly: this code is serial, so each core performs the same calculation … I see the following times printed on my screen: 3.220 s, 2.927 s, 3.211 s—each is from a separate process running the code in a serial fashion.
How can we make this code parallel and faster?
Parallelizing our slow series: non-scalable version
Let’s restart Julia with julia (single control process) and add 2 worker processes:
using Distributed
addprocs(2)
workers()
We need to redefine digitsin() everywhere, and then let’s modify slow() to compute a partial sum:
@everywhere function slow(n::Int, digits::Int, taskid, ntasks) # two additional arguments
println("running on worker ", myid())
total = 0.0
@time for i in taskid:ntasks:n # partial sum with a stride `ntasks`
if !digitsin(digits, i)
total += 1.0 / i
end
end
return(total)
end
Now we can actually use it:
# slow(Int64(10), 9, 1, 2) # precompile the code
precompile(slow, (Int, Int, Int, Int))
a = @spawnat :any slow(Int64(1e8), 9, 1, 2)
b = @spawnat :any slow(Int64(1e8), 9, 2, 2)
print("total = ", fetch(a) + fetch(b)) # 13.277605949852546
For timing I got 1.30 s and 1.66 s, running concurrently, which is a 2X speedup compared to the serial run—this is great! Notice that we received a slightly different numerical result, due to a different order of summation.
However, our code is not scalable: it is limited to a small number of sums each spawned with its own Future reference. If we want to scale it to 100 workers, we’ll have a problem.
How do we solve this problem—any idea before I show the solution in the next section?
Distributed.jl: three scalable versions of the slow series
Solution 1: an array of Future references
We could create an array (using array comprehension) of Future references and then add up their respective results. An array comprehension is similar to Python’s list comprehension:
a = [i for i in 1:5]; # array comprehension in Julia
typeof(a) # 1D array of Int64
We can cycle through all available workers:
[w for w in workers()] # array of worker IDs
[(i,w) for (i,w) in enumerate(workers())] # array of tuples (counter, worker ID)
Exercise “Distributed.3”
Using this syntax, construct an array
rof Futures, and then get their results and sum them up withprint("total = ", sum([fetch(r[i]) for i in 1:nworkers()]))You can do this exercise using either the array comprehension from above, or the good old
forloops.
With two workers and two CPU cores, we should get times very similar to the last run. However, now our code can scale to much larger numbers of cores!
Exercise “Distributed.4”
If you did the previous exercise with an interactive job, now submit a Slurm batch job running the same code on 4 CPU cores. Next, try 8 cores. Did your timing change?
Solution 2: parallel for loop with summation reduction
Unlike the Base.Threads module, Distributed provides a parallel loop with reduction. This means that we can
implement a parallel loop for computing the sum. Let’s write parallelFor.jl with this version of the function:
function slow(n::Int64, digits::Int)
@time total = @distributed (+) for i in 1:n
!digitsin(digits, i) ? 1.0 / i : 0
end
println("total = ", total);
end
A couple of important points:
- We don’t need
@everywhereto define this function. It is a parallel function defined on the control process, and running on the control process. - The only expression inside the loop is the compact if/else statement. Consider this:
1==2 ? println("Yes") : println("No")
The outcome of the if/else statement is added to the partial sums at each loop iteration, and all these partial sums are added together.
Now let’s measure the times:
# slow(10, 9)
precompile(slow, (Int, Int))
slow(Int64(1e8), 9) # total = 13.277605949855722
Exercise “Distributed.5”
Switch from using
@timeto using@btimein this code. What changes did you have to make?
This will produce the single time for the entire parallel loop (1.498s in my case).
Exercise “Distributed.6”
Repeat on 8 CPU cores. Did your timing improve?
I tested this code (parallelFor.jl) on Cedar with v1.5.2 and n=Int64(1e9):
#!/bin/bash
#SBATCH --ntasks=... # number of MPI tasks
#SBATCH --cpus-per-task=1
#SBATCH --nodes=1-1 # change process distribution across nodes
#SBATCH --mem-per-cpu=3600M
#SBATCH --time=0:5:0
#SBATCH --account=...
module load julia
echo $SLURM_NODELIST
# comment out addprocs() in the code
julia -p $SLURM_NTASKS parallelFor.jl
| Code | Time |
|---|---|
| serial | 48.2s |
| 4 cores, same node | 12.2s |
| 8 cores, same node | 7.6s |
| 16 cores, same node | 6.8s |
| 32 cores, same node | 2.0s |
| 32 cores across 6 nodes | 11.3s |
Solution 3: use pmap to map arguments to processes
Let’s write mappingArguments.jl with a new version of slow() that will compute partial sum on each worker:
@everywhere function slow((n, digits, taskid, ntasks)) # the argument is now a tuple
println("running on worker ", myid())
total = 0.0
@time for i in taskid:ntasks:n # partial sum with a stride `ntasks`
!digitsin(digits, i) && (total += 1.0 / i) # compact if statement (similar to bash)
end
return(total)
end
and launch the function on each worker:
slow((10, 9, 1, 1)) # package arguments in a tuple; serial run
nw = nworkers()
args = [(Int64(1e8), 9, j, nw) for j in 1:nw] # array of tuples to be mapped to workers
println("total = ", sum(pmap(slow, args))) # launch the function on each worker and sum the results
These two syntaxes are equivalent:
sum(pmap(slow, args))
sum(pmap(x->slow(x), args))
We see the following times from individual processes:
From worker 2: running on worker 2
From worker 3: running on worker 3
From worker 4: running on worker 4
From worker 5: running on worker 5
From worker 2: 0.617099 seconds
From worker 3: 0.619604 seconds
From worker 4: 0.656923 seconds
From worker 5: 0.675806 seconds
total = 13.277605949854518
Hybrid parallelism
Here is a simple example of a hybrid multi-threaded / multi-processing code contributed by Xavier Vasseur following the October 2021 workshop:
using Distributed
@everywhere using Base.Threads
@everywhere function greetings_from_task(())
@threads for i=1:nthreads()
println("Hello from thread $(threadid()) on proc $(myid())")
end
end
args_pmap = [() for j in workers()];
pmap(x->greetings_from_task(x), args_pmap)
Save this code as hybrid.jl and then run it specifying the number of workers with -p and the number of threads per
worker with -t flags:
[~/tmp]$ julia -p 4 -t 2 hybrid.jl
From worker 5: Hello, I am thread 2 on proc 5
From worker 5: Hello, I am thread 1 on proc 5
From worker 2: Hello, I am thread 1 on proc 2
From worker 2: Hello, I am thread 2 on proc 2
From worker 3: Hello, I am thread 1 on proc 3
From worker 3: Hello, I am thread 2 on proc 3
From worker 4: Hello, I am thread 1 on proc 4
From worker 4: Hello, I am thread 2 on proc 4
DistributedArrays.jl
DistributedArrays package provides DArray object that can be split across several processes (set of workers), either on the same or multiple nodes. This allows use of arrays that are too large to fit in memory on one node. Each process operates on the part of the array that it owns – this provides a very natural way to achieve parallelism for large problems.
- Each worker can read any elements using their global indices
- Each worker can write only to the part that it owns automatic parallelism and safe execution
DistributedArrays is not part of the standard library, so usually you need to install it yourself (it will
typically write into ~/.julia/environments/versionNumber directory):
] add DistributedArrays
We need to load DistributedArrays on every worker:
using Distributed
addprocs(4)
@everywhere using DistributedArrays
n = 10
data = dzeros(Float32, n, n); # distributed 2D array of 0's
data # can access the entire array
data[1,1], data[n,5] # can use global indices
data.dims # global dimensions (10, 10)
data[1,1] = 1.0 # error: cannot write from the control process!
@spawnat 2 data.localpart[1,1] = 1.5 # success: can write locally
data
Let’s check data distribution across workers:
for i in workers()
@spawnat i println(localindices(data))
end
rows, cols = @fetchfrom 3 localindices(data)
println(rows) # the rows owned by worker 3
We can only write into data from its “owner” workers using local indices on these workers:
@everywhere function fillLocalBlock(data)
h, w = localindices(data)
for iGlobal in h # or collect(h)
iLoc = iGlobal - h.start + 1 # always starts from 1
for jGlobal in w # or collect(w)
jLoc = jGlobal - w.start + 1 # always starts from 1
data.localpart[iLoc,jLoc] = iGlobal + jGlobal
end
end
end
for i in workers()
@spawnat i fillLocalBlock(data)
end
data # now the distributed array is filled
@fetchfrom 3 data.localpart # stored on worker 3
minimum(data), maximum(data) # parallel reduction
One-liners to generate distributed arrays:
a = dzeros(100,100,100); # 100^3 distributed array of 0's
b = dones(100,100,100); # 100^3 distributed array of 1's
c = drand(100,100,100); # 100^3 uniform [0,1]
d = drandn(100,100,100); # 100^3 drawn from a Gaussian distribution
d[1:10,1:10,1]
e = dfill(1.5,100,100,100); # 100^3 fixed value
You can find more information about the arguments by typing ?DArray. For example, you have a lot of control over the
DArray’s distribution across workers. Before I show the examples, let’s define a convenient function to show the array’s
distribution:
function showDistribution(x::DArray)
for i in workers()
@spawnat i println(localindices(x))
end
end
nworkers() # 4
data = dzeros((100,100), workers()[1:2]); # define only on the first two workers
showDistribution(data)
square = dzeros((100,100), workers()[1:4], [2,2]); # 2x2 decomposition
showDistribution(square)
slab = dzeros((100,100), workers()[1:4], [1,4]); # 1x4 decomposition
showDistribution(slab)
You can take a local array and distribute it across workers:
e = fill(1.5, (10,10)) # local array
de = distribute(e) # distribute `e` across all workers
showDistribution(de)
Exercise “DistributedArrays.1”
Using either
toporhtopcommand on the training cluster, study memory usage with DistributedArrays. Are these arrays really distributed across processes? Use a largish array for this: large enough to spot memory usage, but not too large not to exceed physical memory and not to affect other participants (especially if you do this on the login node - which you should not).
Building a distributed array from local pieces 1
Let’s restart Julia with julia (single control process) and load the packages:
using Distributed
addprocs(4)
using DistributedArrays # important to load this after addprocs()
@everywhere using LinearAlgebra
We will define an 8x8 matrix with the main diagonal and two off-diagonals (tridiagonal matrix). The lines show our matrix distribution across workers:
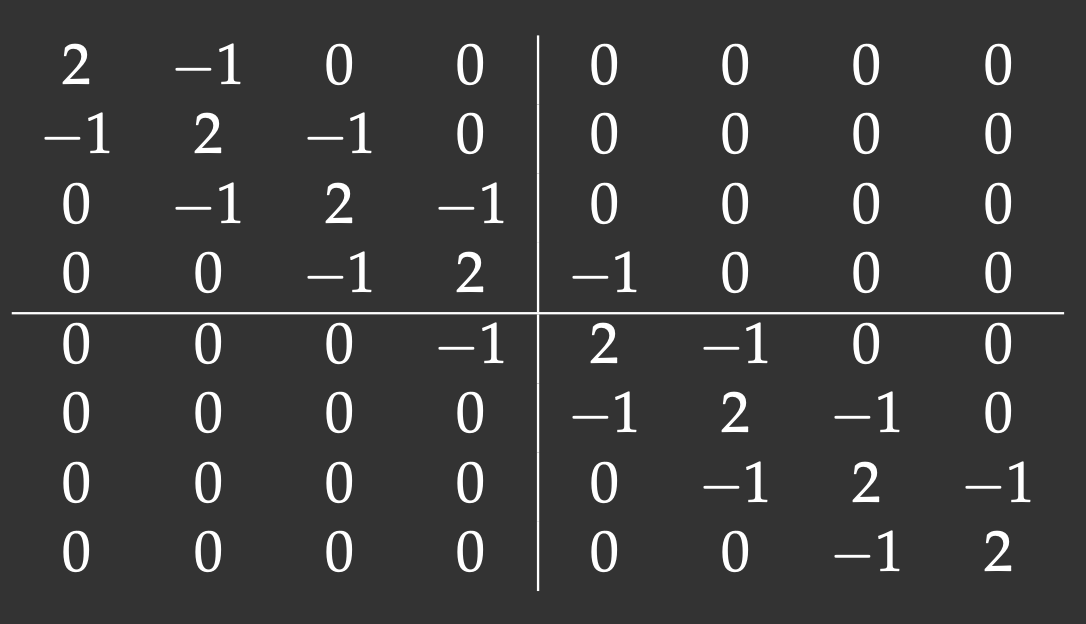
Notice that with the 2x2 decomposition two of the 4 blocks are also tridiagonal matrices. We’ll define a function to initiate them:
@everywhere function tridiagonal(n)
la = zeros(n,n)
la[diagind(la,0)] .= 2. # diagind(la,k) provides indices of the kth diagonal of a matrix
la[diagind(la,1)] .= -1.
la[diagind(la,-1)] .= -1.
return la
end
We also need functions to define the other two blocks:
@everywhere function upperRight(n)
la = zeros(n,n)
la[n,1] = -1.
return la
end
@everywhere function lowerLeft(n)
la = zeros(n,n)
la[1,n] = -1.
return la
end
We use these functions to define local pieces on each block and then create a distributed 8x8 matrix on a 2x2 process grid:
d11 = @spawnat 2 tridiagonal(4)
d12 = @spawnat 3 lowerLeft(4)
d21 = @spawnat 4 upperRight(4)
d22 = @spawnat 5 tridiagonal(4)
d = DArray(reshape([d11 d12 d21 d22],(2,2))) # create a distributed 8x8 matrix on a 2x2 process grid
d
Exercise “DistributedArrays.2”
At this point, if you redefine
showDistribution()(need to do this only on the control process!), most likely you will see no output if you runshowDistribution(d). Any idea why?
Parallelizing the Julia set with DistributedArrays
How would we parallelize this problem with multi-processing? We have a large array, so we can use DistributedArrays and compute it in parallel. Here are the steps:
- Load
Distributedon the control process. - Load
DistributedArrayson all processes. stabilityarray should be distributed:
stability = dzeros(Int32, height, width); # distributed 2D array of 0's
- Define function
pixel()on all processes. - Create
fillLocalBlock(stability)to compute local piecesstability.localparton each worker in parallel. If you don’t know where to start, begin with checking the complete example withfillLocalBlock()from the previous section. This function will cycle through all local indiceslocalindices(stability). This function needs to be defined on all processes. - Replace the loop
@btime for i in 1:height, j in 1:width
point = (2*(j-0.5)/width-1) + (2*(i-0.5)/height-1)im
stability[i,j] = pixel(point)
end
with
@btime @sync for w in workers()
@spawnat w fillLocalBlock(stability)
end
- Why do we need
@syncin the previousforblock? - To the best of my knowledge, both Plots’
heatmap()and NetCDF’sncwrite()are serial in Julia, and they cannot take distributed arrays. How do we convert a distributed array to a local array to pass to one of these functions? - Is your parallel code faster?
Results for 1000^2
Finally, here are my timings on (some old iteration of) the training cluster:
| Code | Time on login node (p-flavour vCPUs) | Time on compute node (c-flavour vCPUs) |
|---|---|---|
julia juliaSetSerial.jl (serial runtime) |
147.214 ms | 123.195 ms |
julia -p 1 juliaSetDistributedArrays.jl (on 1 worker) |
157.043 ms | 128.601 ms |
julia -p 2 juliaSetDistributedArrays.jl (on 2 workers) |
80.198 ms | 66.449 ms |
julia -p 4 juliaSetDistributedArrays.jl (on 4 workers) |
42.965 ms | 66.849 ms |
julia -p 8 juliaSetDistributedArrays.jl (on 8 workers) |
36.067 ms | 67.644 ms |
Lots of things here to discuss!
One could modify our parallel code to offload some computation to the control process (not just compute on workers as we do now), so that you would see speedup when running on 2 CPUs (control process + 1 worker).
External links
- Julia at Scale forum
- Think Julia: How to Think Like a Computer Scientist by Ben Lauwens and Allen Downey is a good introduction to basic Julia for beginners
- Baolai Ge’s (SHARCNET) November 2020 webinar Julia: Parallel computing revisited
- WestGrid’s March 2021 webinar Parallel programming in Julia
- WestGrid’s February 2022 webinar ThreadsX.jl: easier multithreading in Julia
- Julia performance tips
- How to optimise Julia code: A practical guide
- A Deep Introduction to JIT Compilers
-
This example was adapted from Baolai Ge’s (SHARCNET) presentation. ↩︎